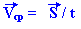|
|
ОТВЕТЫ.
5. Чему равна средняя скорость?
Строго говоря, средняя скорость автомобиля в соответствии с формулой:
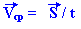равна нулю, поскольку, выехав из пункта А, он в конечно счете туда же и возвратился (т. е. перемещение S = 0).
Однако в повседневной жизни под средним значением скорости подразумевают среднее значение её модуля V cp , определить которое можно, разделив пройденный путь на время движения. Рассмотрим, чему же он равен.
Напрашивающийся и обычно даваемый ответ 50 км/ч не является правильным. В самом деле, обозначим расстояние между пунктами А и В через l. Тогда время, затрачиваемое автомобилем на переезд из А в В, будет равно:
t 1 = l / V 1 .
Обратный переезд потребует времени:
t 2 = l / V 2 .
А на весь путь туда и обратно будет затрачено:
t = t 1 + t 2 = l / V 1 + l / V 2 = l ( V 1 + V 2 ) / V 1 V 2
После этого средняя скорость:
V cp = 2 l / t .
или с учётом предыдущей формулы:
V cp = 2 ( V 1 + V 2 ) / V 1 V 2
Подставляя сюда значение скоростей V1 и V2, получим для средней скорости значение 48 км/ч.
Формулу для вычисления средней скорости в данном случае можно представить в следующем виде:
1/V cp = 1/2 ( 1 /V1 + 1/V2 )
Величина Vcp, определяемая таким образом, носит название среднего гармонического величин V1 и V2 . Следовательно, среднее гармоническое двух данных есть число, обратное среднему арифметическому чисел, в свою очередь обратных заданным числам.
Среднее гармоническое чисел а и Ь можно построить геометрически.
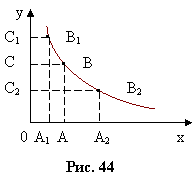
На рисунке 44 представлена гипербола, выражающая график функции у =1/x. Отложим на оси Ох отрезки ОА1=а и ОА2=b. После этого проведем из точек и А2 нормали к оси Ох до пересечения с гиперболой в точках В1 и В2. Далее опустим из них перпендикуляры ВС1 и В2С2 на ось Оу и расстояние С1С2 разделим на две равные части. Если из полученной точки С восставить перпендикуляр СВ до пересечения с гиперболой, а из точки В провести нормаль ВА к оси Ох, то длина h отрезка ОА и будет равна среднему гармоническому чисел а и Ь, что непосредственно следует из системы равенств:
А1В1 = 1/a,
А2В2 = 1/b,
AB = 1/h,
АВ = 1/2 (А1В1+А2В2).
Можно показать, что между средним гармоническим h чисел а и Ь, их средним геометрическим g = √аЬ и средним арифметическим m = (а + b) /2 существует соотношение:
m ≥ g ≥ h
(знак равенства имеет место в случае а = Ь).
Средняя скорость лишь иногда равна среднему арифиетическому, например при равноускоренном движении (движении с постоянным ускорением) ; для данного же случая средняя скорость выражается как среднее гармоническое скоростей V1 , и V2.
|
|