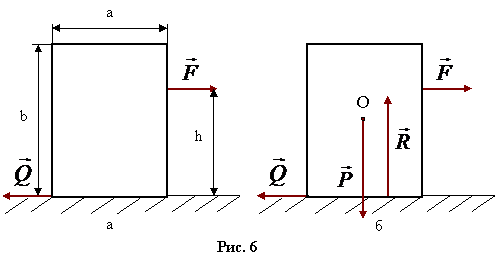
Начнём задачу несколько издалека. Пусть на горизонтальной площадке стоит прямоугольный брусок, имеющий высоту b и ширину а (толщина несущественна). Приложим к нему на высоте h направленную горизонтально силу F Одновременно появится сила трения Q, равная по модулю F, если последняя не превышает максимального значения силы трения покоя:
Поскольку силы F и Q не лежат на одной прямой, они создают момент F×h, стремящийся опрокинуть брусок по часовой стрелке. Чем больше модуль силы F и чем выше она приложена, тем больше опрокидывающий момент.
Если бы существовала только пара сил F и Q, брусок опрокидывался бы при сколь угодно малой приложенной силе F. На самом же деле, чтобы опрокннуть брусок, сила должна иметь строго определенную величину. Следовательно, существует момент, препятствующий опрокидыванию. Происхождение момента легко понять.
Момент пары сил F и Q стремится приподнять левый край бруска и плотнее прижать к площадке его правую половину. В результате сила реакции опоры R, приложенная вертикально вверх к основанию бруска и равная. по модулю его силе тяжести Р, уже не будет проходить через центр нижней грани и центр тяжести бруска, а сместится несколько вправо (рис. 6, б). Чем больше модуль силы Р, тем больше опрокидываюший момент, тем дальше вправо должна сместиться сила R, чтобы брусок не опрокинулся. В зависимости от соотношения между величинами а, Ь, h и F могут быть два случая:
1. Сила F достигнет по модулю значения Qмакс = k×P прежде, чем R выйдет за пределы контура опоры. Тогда брусок придет в движение по плоскости, не опрокинувшись.
2. До того как F сравняется с k×P, реакция опоры подойдет к правой границе нижней плоскости бруска.После этого момент пары сил R и Р уже не сможет больше компенсировать момента пары F и Q, и брусок опрокинется.
Отсюда вытекает, между прочим, несложный способ определения коэффициента трения между бруском и поверхностью, на которой он стоит.
Приложим силу F, чуть-чуть превышающую k×P, у самой нижней грани бруска. Он придет тогда в равномерное движение. Будем постепенно поднимать точку приложения силы F (все это легко проделать, вооружившись коробкой из-под туфель). Тогда при некоторой высоте брусок, не приходя в поступательное движение начнет опрокидываться.
Запишем "граничные условия", при которых наблюдается переход от одного случая к другому, т.е. равенство сил и моментов (последние будем определять относительно оси, проходящей через центр тяжести бруска и перпендикулярной плоскости рисунка, считая положительными моменты, вращающие брусок по часовой стрелке, и отрицательными - стремящиеся повернуть его в противоположном направлении):
Q – F = 0, (F = k×P)
F×(h – b/2) + Q ×b/2 – R ×a/2 – P 0 = 0
Сформулируем теперь софизм. Пусть на горизонтальной площадке помещен не брусок, а шар. Он имеет с площадкой единственную точку соприкосновения. Поэтому сила реакции опоры и сила тяжести тела всегда должны проходить через нее. Значит, момент пары сил R и Р (или сумма моментов этих сил относительно точки соприкосновения) равен нулю. Следовательно, любая, даже очень малая, сила, приложенная к шару, должна привести его во вращение. Иными словами, коэффициент трения качения всегда должен равняться нулю! На самом же деле, он, хотя и значительно меньше коэффициента трения скольжения, однако нулю все же не равен.
Где же ошибка в наших рассуждениях? Ответ здесь.